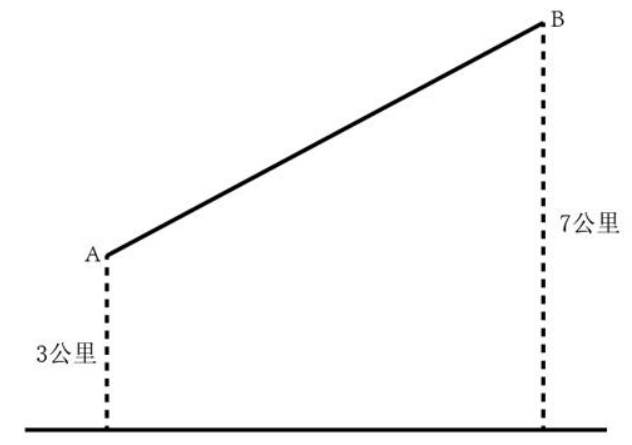
（2023陕西省考96题）A、B两村在一条笔直公路的同侧，到公路的垂直距离分别是3公里和7公里，两村相距8.5公里，现需在公路边建一个物资集散中心，为节约物资配送成本，集散中心到两个村的直线路程之和应尽可能小，若货车的速度约为60公里/小时，那么货车从集散中心出发，到两村送货后返回中心，路途所花费的最少时间为：

A.18分钟

B.21分钟

C.24分钟

D.27分钟

参考答案：B

参考解析：以两点之间直线最短作为解题思路。如图所示：四边形ADNM和为矩形，四边形A1D1NM与其关于公路MN对称。连接A1、B，交MN于点O，根据两点之间线段最短，可知将物资集散中心修建在O点时，到两村的直线路程之和最小。

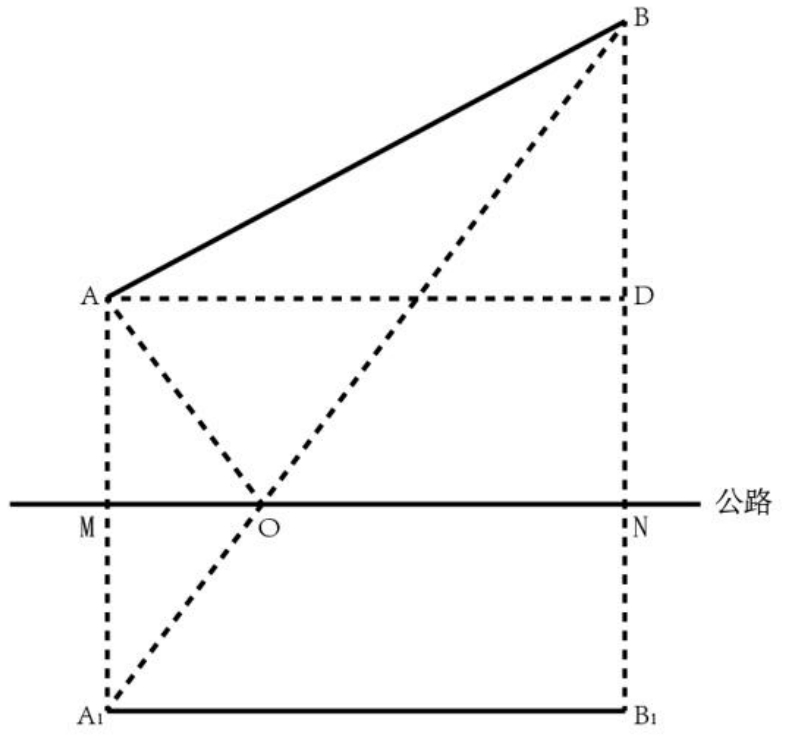
已知AM=3，BN=7，AB=8.5，则BD=4，在ABD三角形中，计算AD：

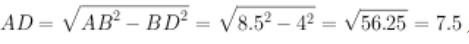
对应的，A1B1=AD=7.5。在三角形A1B1B中，BB1=10，计算A1B：

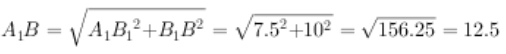
根据题目信息，货车从集散中心出发，到两村送货后返回中心，经历的路程=A1B+AB=12.5+8.5=21（公里）。

若货车的速度约为60公里/小时，走完21公里路程需要(21/60)*60=21分钟。