排列组合计数问题,比较容易出错。出错的原因在于计数时要么弄重了,要么弄漏了。熟悉相关的模型和方法,可以让解题思路简洁明了,提升解题速度并且避免出错。一、捆绑法
捆绑法用来处理相邻问题。在排列计数问题中,把需要相邻的元素“捆绑”在一起,视作一个元素参与排列。注意点:捆绑的元素最后还要“解绑”,把捆在一起的几个元素进行排列。

二、插空法
插空法用来处理不相邻问题。不能相邻的元素通常最后参与排列,通过插空的方式放在已排的元素之间。

三、隔板法
隔板法用来将相同的元素分组,并且每组至少有一个元素。

隔板法一般适用于每组至少一个元素的情况,如果没有这个限定条件,允许有空盒的情况下,那么此时隔板法就不适用了,那这时该如何解决呢?
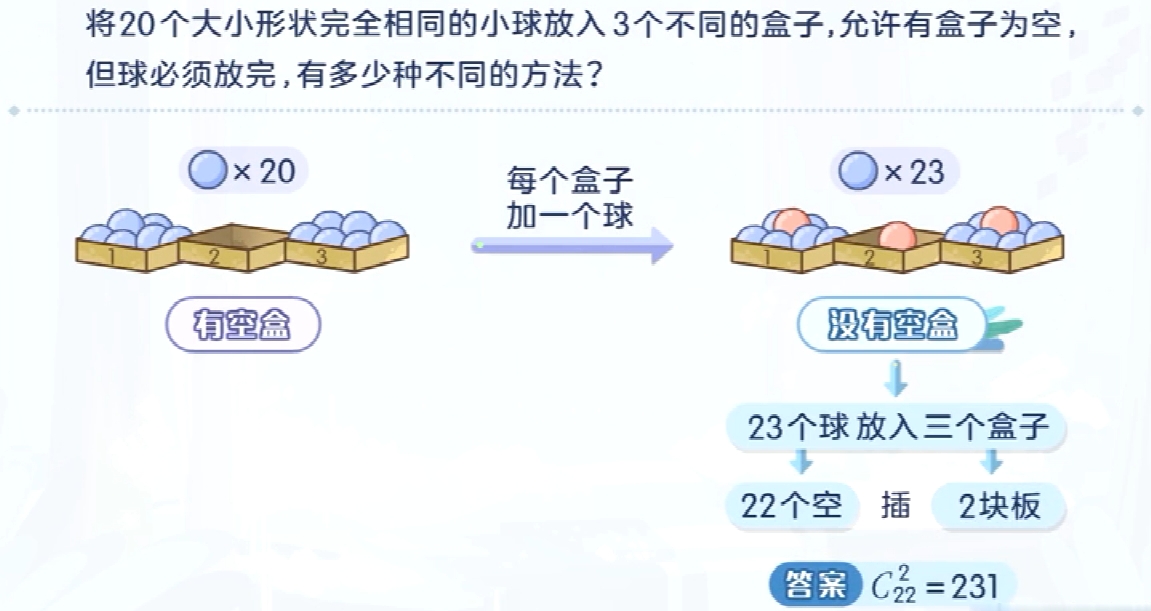
再来看一种特殊的情况:
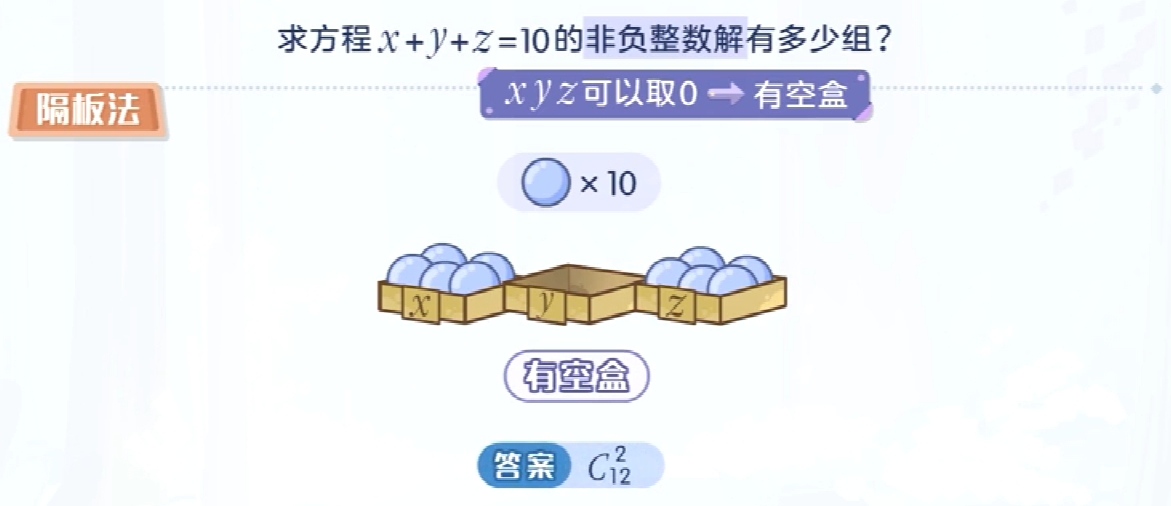
四、分堆问题
平均分堆问题,因为要排除重复问题,一般若有平均分n组,则要除以n个元素的全排列数。
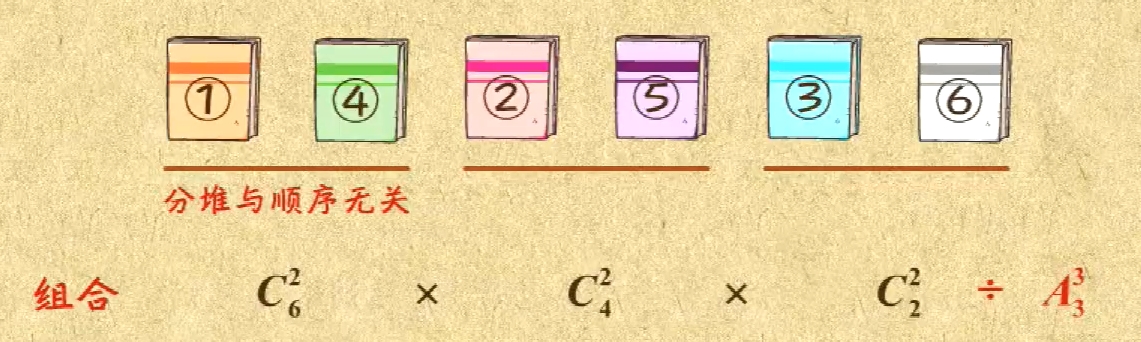
增加难度:



