一、什么是RMSE

RMSE，或均方根误差（Root Mean Square Error），是一种衡量模型预测值与真实值之间差异的常用指标。它通过计算预测值与真实值之间误差的平方，然后取平均后开平方来反映模型的性能。RMSE越小，表示模型的预测效果越好。

RMSE的公式为：

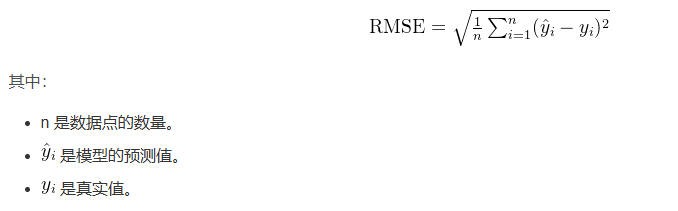
二、Python中RMSE的计算方法

在Python中，我们可以通过多种方法计算RMSE，包括手动计算和使用库函数。以下是两种方法的介绍。

方法一：手动计算RMSE

首先，我们可以通过Python的基本数学运算来手动计算RMSE。具体步骤如下：

1. 计算每个实际值和预测值之间的差异。
2. 将这些差异平方。
3. 计算平方差的平均值。
4. 对平均值取平方根，得到RMSE。

下面是手动计算RMSE的示例代码：

import numpy as np

# 真实值
y_true = np.array([3, -0.5, 2, 7])
# 预测值
y_pred = np.array([2.5, 0.0, 2, 8])

# 计算RMSE
def calculate_rmse(y_true, y_pred):
    # 计算误差
    error = y_true - y_pred
    # 计算误差的平方
    error_squared = error ** 2
    # 计算均值
    mean_error_squared = np.mean(error_squared)
    # 取平方根
    rmse = np.sqrt(mean_error_squared)
    return rmse

result_rmse = calculate_rmse(y_true, y_pred)
print("RMSE:", result_rmse)

方法二：使用库函数计算RMSE

Python的scikit-learn库提供了一个现成的函数来计算RMSE，使用起来更加方便。可以利用mean_squared_error函数计算均方误差，然后再开平方得到RMSE。

示例代码如下：

from sklearn.metrics import mean_squared_error
import numpy as np

# 真实值
y_true = np.array([3, -0.5, 2, 7])
# 预测值
y_pred = np.array([2.5, 0.0, 2, 8])

# 计算均方误差
mse = mean_squared_error(y_true, y_pred)
# 取平方根得到RMSE
rmse = np.sqrt(mse)
print("RMSE:", rmse)

三、总结

无论使用手动计算还是使用库函数，RMSE都是一个直观且易于理解的指标，可以有效地评估模型的预测能力。对于实际的项目开发，建议使用scikit-learn库中的函数，因为它不仅可以节省编写代码的时间，还能减少误差，提高代码的可读性和可维护性。

RMSE计算流程图

为了更好地理解RMSE的计算过程，下面我们展示一个流程图：

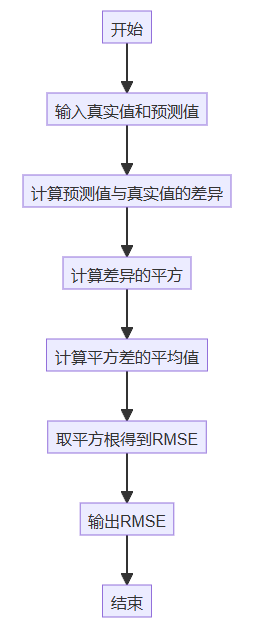
通过上述代码示例和流程图，我们可以清晰地了解如何在Python中计算RMSE。这一指标在数据科学和机器学习建模中非常重要，它帮助我们量化预测与真实数据的偏差，指导模型的进一步优化与调整。

参考资料：rmse怎么计算Python_mob64ca12e7f20c的技术博客_51CTO博客